列空间和零空间

列空间

同一向量空间的子空间\(S\)和\(T\)的交集也是一个子空间。

\(A的列空间是所有列向量的线性组合\)。

求\(A\)矩阵的列空间就等同于问“方程\(Ax=b\)对于任意向量x，会得到哪些b？”

我们只能在\(b\)向量在\(A\)矩阵列空间的时候求解出方程\(Ax=b\)。

但是，原矩阵有一个问题：我们可以“丢掉”任意一列，然后得到完全相同的向量空间。因为第三列是前两列的和。如果我们有了前两列，第三列就可以用前两列的某种线性变换表示，第三列就没有任何“新的贡献”。也就是说，第三列是和前两列线性相关的。

零空间（Nullspace）

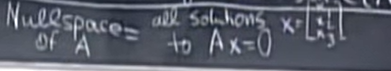
零空间指的是所有能满足\(Ax=0\)的\(x\)组成的向量空间。

原矩阵的零空间就是所有这种形式的矩阵组成的\(R^3\)的子空间。它是一条在\(R^3\)空间的直线。

总结

这节课主要讲解了得到子空间的两种思路：

1. 找到矩阵的列的线性组合，所有的线性组合构成了一个子空间。（列空间）
2. 找到使\(Ax=0\)方程成立的所有向量\(x\)，所有的\(x\)构成了一个子空间。（零空间）