找到Ax=b的全部解

先解出一个特殊解:\(x_p\),然后你会发现这个解加上任何一个位于\(Nullspace\)中的向量都是一个解(因为零空间是所有满足\(Ax=0\)的\(x\)集合),也就是说,\(x=x_p+x_n\)。
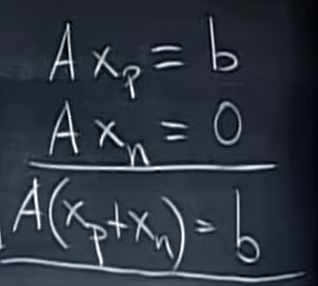
接着,使用上节课的思路:所有位于零空间的向量就是“把一个自由变量设为1,其他自由变量为0得到的\(Ax=0\)的解”的所有线性组合:
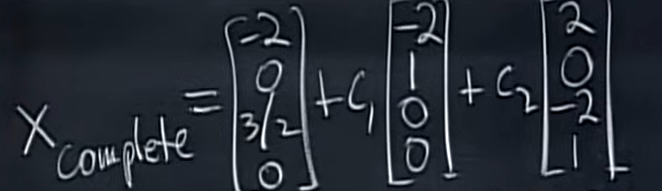
如果我们尝试把它的解集画出来,大概长这样:
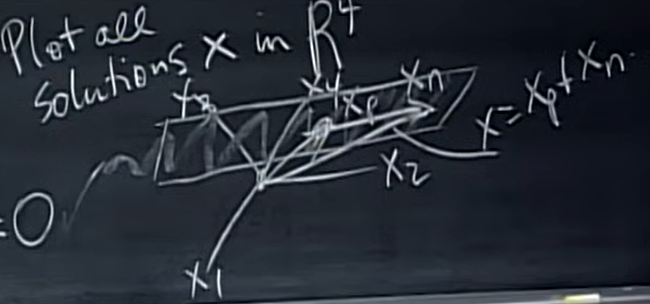
它是一个穿过\(x_p\)的平面,但是不一定穿过原点,因此它不是子空间。
满秩矩阵

(如果\(r=n\),则它是一个列满秩矩阵,解的数量为\(0\)或\(1\))
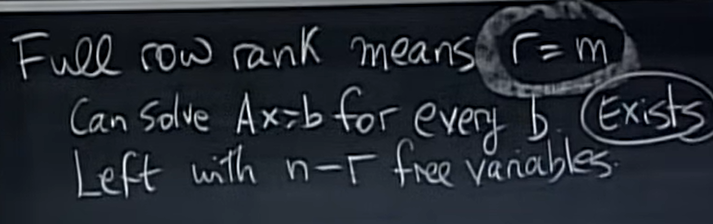
(如果\(r=m\),则它是一个行满秩矩阵,对于任何\(b\),都存在解。留下了\(n-r\)个自由变量,如果存在自由变量,即\(n-r>0\),就有无穷多解。)
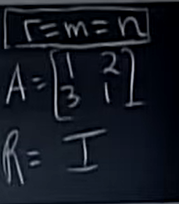
如果\(r=m=n\),说明它是可逆矩阵,即有唯一解。
总结
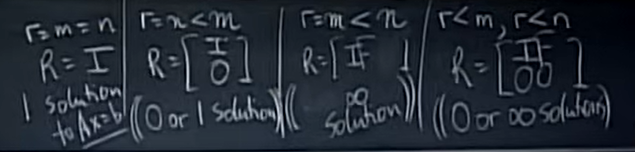
| 情形 | 条件 | 行最简形式 R | 解的个数 |
|---|---|---|---|
| 1 | \(r=m=n\) | \(R=I\) | 唯一解(1 个) |
| 2 | \(r=n<m\) | \(R=\begin{bmatrix}I\\0\end{bmatrix}\) | 0 个或 1 个解 |
| 3 | \(r=m<n\) | \(R=\begin{bmatrix}I & F\end{bmatrix}\) | 无穷多解 |
| 4 | \(r<m, r<n\) | \(R=\begin{bmatrix}I&F\\0&0\end{bmatrix}\) | 0 个或无穷多解 |
发表回复