矩阵空间

复习一下向量空间（Vector Space）的定义：

向量空间 \(V\) 是一个非空集合，它上的元素称为向量，满足两个运算：加法和数乘，并且得到的结果还在该集合中。

这两个运算必须满足以下 8 条公理（向量空间公理）：

（一）加法的性质u（对任意 \(\mathbf{u}, \mathbf{v}, \mathbf{w} \in V\)）：

1. 交换律： \(\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}\)
2. 结合律：\((\mathbf{u} + \mathbf{v}) + \mathbf{w} = \mathbf{u} + (\mathbf{v} + \mathbf{w})\)
3. 零向量存在性：存在 \(\mathbf{0} \in V\)，使得 \(\mathbf{v} + \mathbf{0} = \mathbf{v}\)
4. 负向量存在性：对每个 \(\mathbf{v} \in V\)，存在 \(-\mathbf{v} \in V\)，使得 \(\mathbf{v} + (-\mathbf{v}) = \mathbf{0}\)

（二）数乘的性质（对任意 \(\mathbf{u}, \mathbf{v} \in V\)）：

5. 结合律：\(a(b \mathbf{v}) = (ab) \mathbf{v}\)
6. 单位元作用：\(1 \cdot \mathbf{v} = \mathbf{v}\)，其中 \(1\) 是乘法单位元
7. 分配律（标量加法）：\(\mathbf{v} = a\mathbf{v} + b\mathbf{v}\)
8. 分配律（向量加法）：\(a(\mathbf{u} + \mathbf{v}) = a\mathbf{u} + a\mathbf{v}\)

矩阵空间的引入

那么，考虑所有\(3 \times 3\)的矩阵，它们其实也构成一个向量空间，因为它们满足上述所有公理。这个向量空间叫做\(3 \times 3\)的矩阵空间，记作\(M_{3 \times 3}(\mathbb R)\)。

\(M_{3 \times 3}(\mathbb R)\)的子空间有：所有\(3 \times 3\)的对称矩阵空间、所有\(3 \times 3\)的上三角矩阵空间等等。

矩阵空间的基

显然，\(M_{3 \times 3}\)的基有\(9\)个。

而\(S\)空间（对称矩阵空间）和\(U\)空间（上三角矩阵空间）作为子空间，它们的维度都是\(6\)。另外，它们的交集维度是\(3\)；它们的和（也就是任意两个的线性组合构成的大空间）的维度是\(9\)，也就是整个空间。

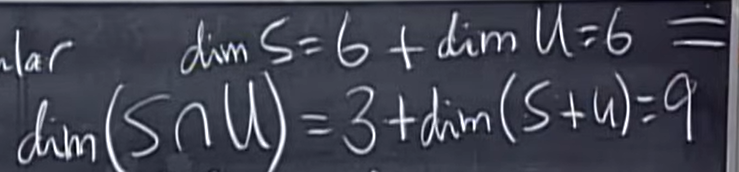
我们很自然地找到了一个公式：\(dim\ S+dim\ U = dim(S\cap U) + dim(S + U)\)