矩阵乘法
若\(AB=C\),则
角度1:
$$C_{i,j}=(row\ i\ of\ A) \cdot (column\ j\ of\ B)$$
角度2,3:

角度4:
首先考虑,用A的一列乘B的一行会得到什么?
这是一个\(m \times 1\)的矩阵乘一个\(1\times p\)的矩阵,所以会得到一个\(m \times p\)的矩阵,并且得到的这个矩阵非常特殊,因为它的行列空间都分别在一条直线上。
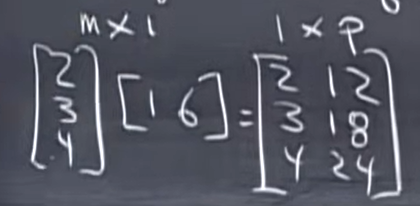
而第4种角度就是:
$$C = \sum_{i=1}^n(column\ i\ of\ A) \cdot (row\ i\ of\ B)$$
角度5:
“分块”
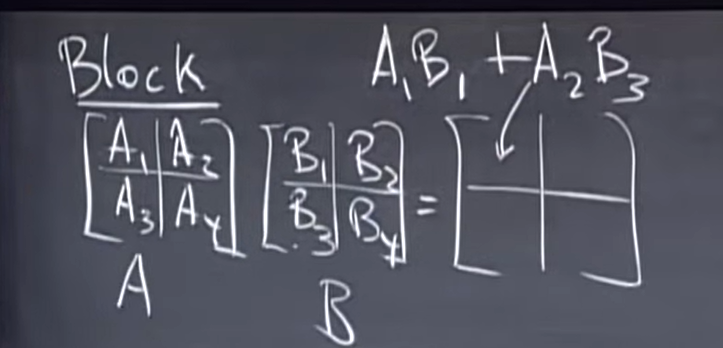
$$C_{ij} = \sum_{k=1}^n A_{ik} B_{kj}$$
这种思想被广泛应用于GPU并行计算等场合。
逆矩阵
一个矩阵的逆矩阵要保证
$$A^{-1}A = I = AA^{-1}$$

但并不是每个矩阵都有逆矩阵,没有逆矩阵的矩阵称为“奇异矩阵”。
首先,如果原矩阵不是方阵,就不存在逆矩阵。
然后,如果存在某个非零向量x,使得\(Ax=0\),A就不存在逆矩阵。因为如果它存在,我们会解出\(x=0\),但实际上x非零。
高斯消元法:
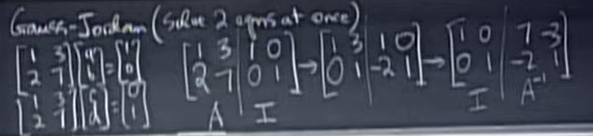
对AI增广矩阵进行若干次行初等变换(就像之前文章说的那样,行初等变换操作就相当于左乘一个初等矩阵,对增广矩阵进行操作是为了方便把等号左右两边同时操作),我们先会得到一个“倒三角形矩阵”(这是因为我们只消除了左下这一个三角形的数);然后,通过回代的方式,只让对角线有数字;最后,把对角线上的数都归一。这样进行若干次行初等变换后,\(A\)变成了\(I\),同理\(I\)就变成了\(A^{-1}\)
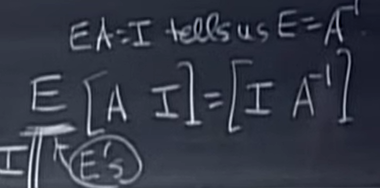
发表回复