从高斯消元到矩阵分解

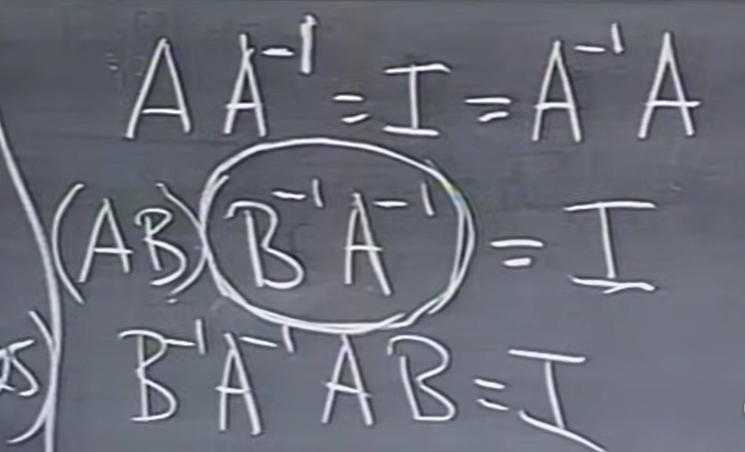
\(AB\)的逆是\(B^{-1}A^{-1}\)，这是很显然的（一个很蠢的类比：你穿上袜子再穿上鞋子的逆是你先脱掉鞋子再脱掉袜子）。

另一个公式：

$$(AB)^T=B^T A^T$$

因此

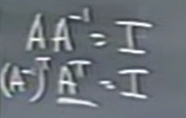
$$(A^{-1})^T=(A^T)^{-1}$$

考虑高斯消元的过程：

（初等矩阵的逆矩阵就是把那个负的变成正的，相当于把减去的那行再加回来）

我们这里已经可以看到L和U的大体“形状”了：L在对角线上全是1，并且是一个正三角形；U是一个倒三角形，对角线上都是我们的“支点”。

三维情况：

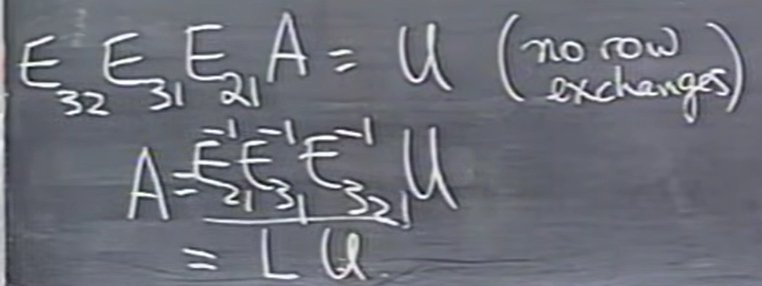
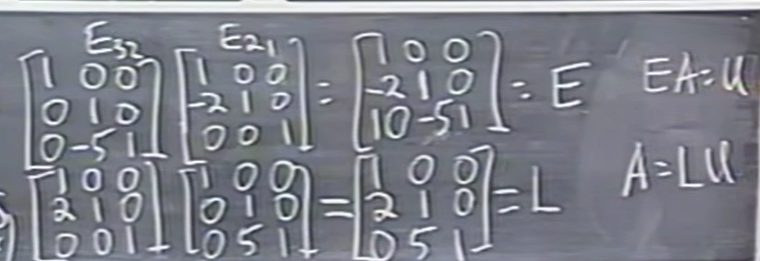
如果没有行交换操作，所有的\(E_{??}^{-1}\)会直接“进入”\(L\)中，我们不需要做任何事情，只需要把改的位置都原样放进\(L\)里，就像上面那样。但是反之，所有\(E_{??}\)相乘得到的\(E\)矩阵，就不能这么操作。因为编号较小的行先改变了，编号较大的行才改变，但是编号较大的行需要使用编号较小的行，但此时它已改变。所以上面这个例子中会产生一个我们不喜欢的\(10\)。

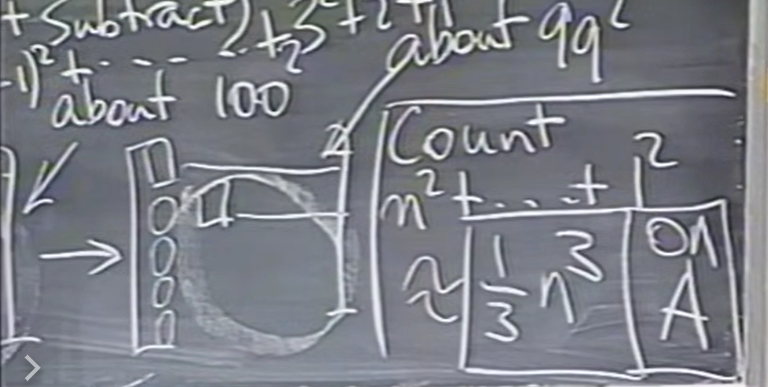
可计算出高斯消元的时间复杂度是\(\frac{1}{3} n^3\)。

行交换的初等矩阵记作\(P\)，而3维中\(P\)的所有组合如下：

一个\(3\times 3\)的矩阵只有6个不同的\(P’s\)。

这些矩阵很特殊：它们互相无论怎么乘，都会得到一个在这个列表中的一个矩阵，同样，它们的逆矩阵也在列表中。这些矩阵组成了一个群（Grup）。并且，\(P^{-1}=P^T\)。