转置，向量空间

接着上节课

其中\(P\)是一个行被重新排列的单位矩阵。

\(n \times n\)的矩阵一共有\(n!\)种\(P\)的组合。

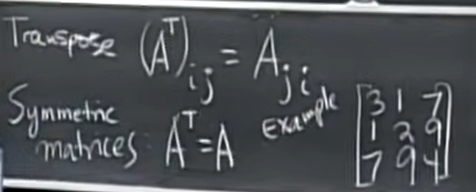
对称矩阵：\(A^T=A\)。

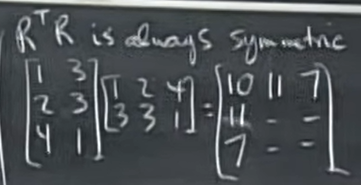
\(RR^T\)永远都是对称矩阵。

向量空间(Vector Space)是指一堆能相互加，也可以把自身乘以一个标量，最终还会得到一个本空间内的向量的东西。此外，它必须满足8条公理。

比如，\(R^N\)空间是一个向量空间，因为对它进行加和数乘操作是封闭的。

一个向量空间中的向量空间叫做子空间（Subspace）。

\(R^2\)的子空间可以是所有位于一条穿过原点的直线上的向量。

但是这个子空间并不是\(R^1\)，因为它里面的向量都有两个分量。

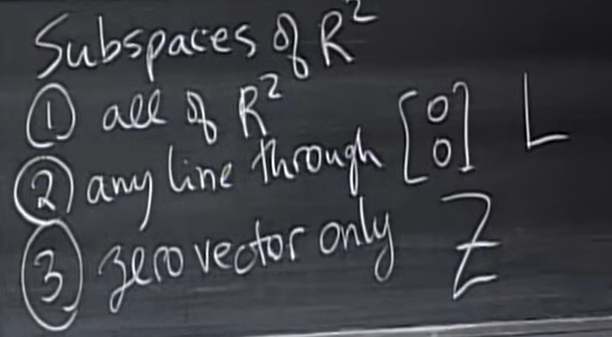
所有的\(R^2\)的子空间：

这个例子中的矩阵的两列的向量，所表示的所有线性组合（即其一的倍数+另一的倍数）被称为列空间(Column space)，顾名思义，就是矩阵的列向量们所张成的一个向量空间，而它们张成的这个列空间一定是\(R^3\)的一个子空间。

也就是说，一个矩阵的列的所有线性组合，张成了一个向量空间，叫做列空间。