秩和简化阶梯型矩阵，N=(-F,I)

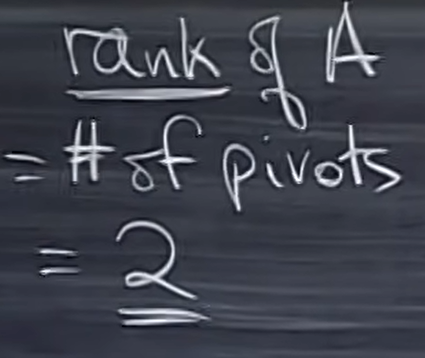
矩阵的秩（Rank）是消元后“枢轴”的位置。

进行前向消元后会得到一个阶梯型矩阵，这个例子中我们得到了2个枢轴列和两个自由列。因为我们可以给\(x_2\)和\(x_4\)分配任意值，然后求解出\(x_1\)和\(x_3\)。

零空间就是所有“特殊解”向量所张成的子空间。“特殊解”的意思是把自由变量们赋值为“其中一个是1，其他是0”的形式所得到的方程组解。

简化阶梯型矩阵：

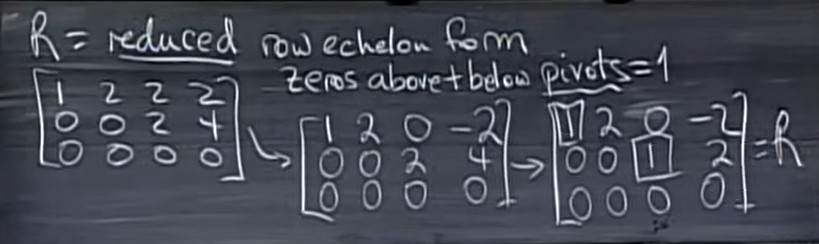
就是每个“枢轴”列只有一个数是\(1\)，其他都是\(0\)的阶梯型矩阵。

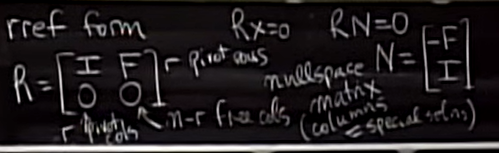
其中\(I\)代表单位矩阵，\(F\)代表自由变量们的行和列“分离”出的子矩阵。