线性无关，空间的基和维度

线性无关的定义

称向量\(x_1,x_2,…,x_n\)是线性无关（Linearly independent）的，当它们的线性组合无法产生\(0\)向量（除了所有系数都是零向量的情况）。反之，则称其为线性相关（Linearly dependent）的。

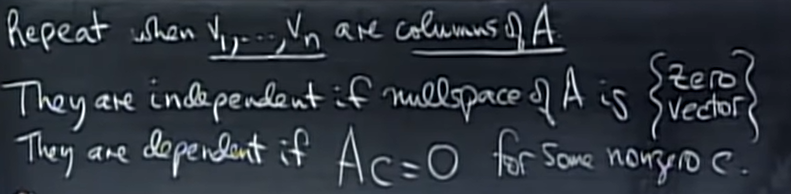
换句话说，线性无关意味着零空间只有零向量；线性相关意味着零空间有非零向量。

空间的基

一个空间的基（Basis）是一些线性无关且能够张成这个空间的向量。

空间的维度

给定一个空间，这个空间的不同的基的向量数量是相同的，而这个数量就是这个空间的维度（Dimension）。

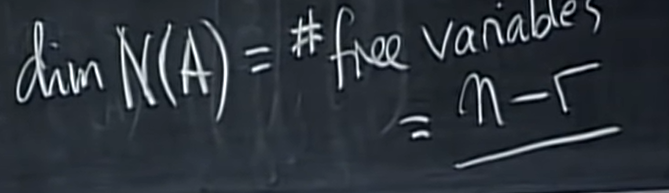
实际上，\(dim(C(A)) = r\)，\(dim(N(A)) = n-r\)。