简介
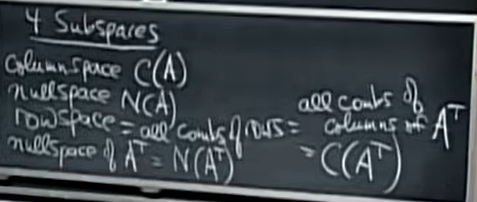
四种子空间分别是:
- 列空间:\(C(A)\),在\(R^m\),维度\(r\)
- 零空间:\(N(A)\),在\(R^n\),维度\(n-r\)
- 行空间:\(C(A^T)\),在\(R^n\),维度\(r\)
- 左零空间:\(N(A^T)\),在\(R^m\),维度\(m-r\)
关于行空间的维度
事实是:\(Dimension\ of\ C(A) = Dimension\ of\ C(A^T) = r\)
一个不太严谨但是很好的说明是:
首先,对\(A\)进行高斯消元,化为主元列只有主元位置是\(1\)的最简形式,此时并不会改变行空间的维度,也不会改变矩阵对应方程组的解集;
我们显然会得到\(r\)个非零行,并且有\(r\)个主元列,因此行空间和列空间的维度都是\(r\)。
关于左零空间
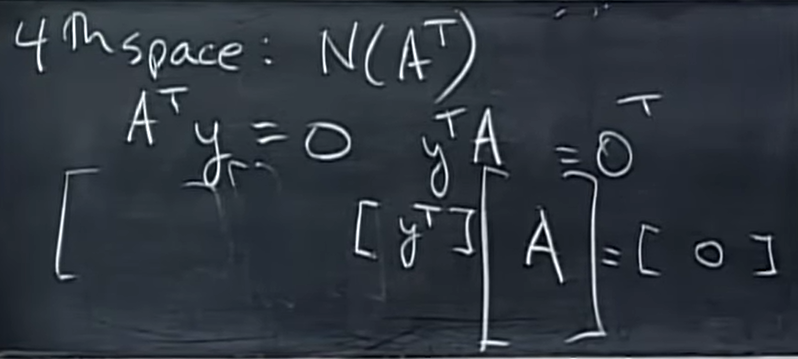
左零空间就是\(N(A^T)\),也就是说,左零空间是满足\(A^T y = 0\)的\(y\)所在的空间,把整个等式左右两边同时转置得到\(y^T A = 0^T\),这是一个行向量左乘一个矩阵等于零行向量,因此叫它“左零空间”。
当我们进行行化简后,得到\(EA = R\)形式:
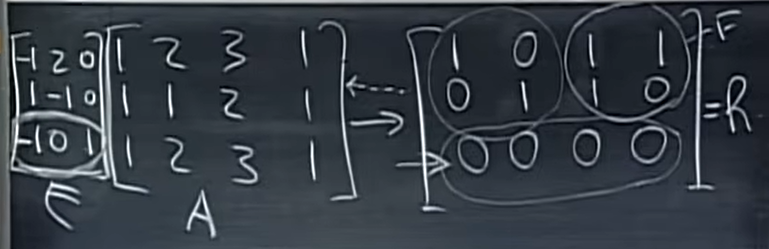
其中\(R\)底部会有一些零行,这些零行正是对应的\(E\)的这些行左乘\(A\)矩阵得到的,也就是说,\(E\)的这些行正是左零空间的基。
总结
现在我们知道了这四种空间,两个在\(R^n\)的空间:行空间和零空间,它们的维度分别是\(r\)和\(n-r\);两个在\(R^m\)的空间:列空间和左零空间,它们的维度分别是\(r\)和\(m-r\)。
发表回复