不定积分:若\(F'(x)=f(x)\),则称函数F(x)是f(x)的一个不定积分。
可积分函数都有无穷多个不定积分,而它们的差异仅仅在常数项上。
微积分基本定理2:
若\(F(x)\)是\(f(x)\)的一个不定积分,则:
$$\int_a^b f(x)\, dx = F(b) – F(a)$$
这意味着我们计算定积分时仅需求不定积分之差。
不定积分:若\(F'(x)=f(x)\),则称函数F(x)是f(x)的一个不定积分。
可积分函数都有无穷多个不定积分,而它们的差异仅仅在常数项上。
微积分基本定理2:
若\(F(x)\)是\(f(x)\)的一个不定积分,则:
$$\int_a^b f(x)\, dx = F(b) – F(a)$$
这意味着我们计算定积分时仅需求不定积分之差。
若\(g’ = f \) ,则称 g 是 f 的一个不定积分(也叫原函数)。由于求导会“吞掉”常数项,因此若g是f的一个不定积分,那么\(g + C \) 一定也是f的一个不定积分(其中C是常数)。更专业地说,所有形如\(g + C \)的函数(一定是f的不定积分)全体构成一个以常数为参数的族。
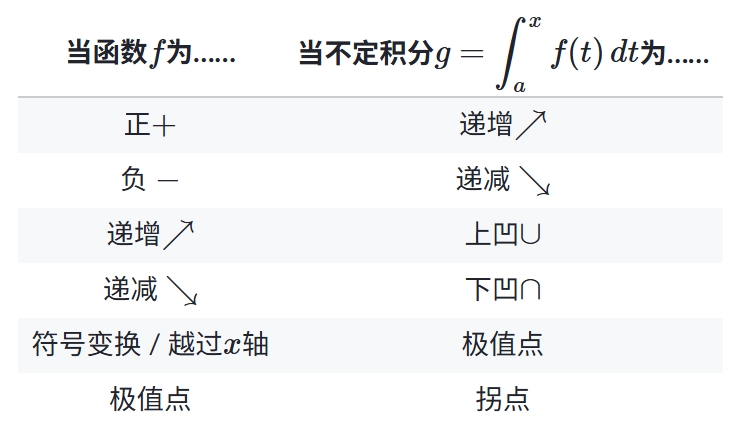
如图列出了一个 f 和 g 的关系,其实和微分中f’和f的关系一样。
微积分基本定理是一个非常重要、优美且符合直觉的定理。它的公式如下:
$$
\frac{d}{dx} \int_a^x f(t) \, dt = f(x)
$$
这意味着,一个函数积分的导数是原函数。
求 \(\frac{d}{dx} \int_2^x cos^2(x) \)
解:
很显然,答案就是里面的原函数,也就是 \(cos^2(x) \) 。
先看题目:
定义 \(f(x) = \int_0^{x^2} sin(x) \) ,求 \(f'(20)\) 。
看起来也可以用该定理求出答案,但是此时积分的上限变成了\(x^2\) ,而不是 \(x\) ,这怎么办呢?
有一个拆分函数的思路可以解决这种问题:
定义
$$g(x) = \int_0^{x} sin(x)$$
$$h(x) = x^2$$
那么
$$f(x) = g(h(x))$$
因此,根据链式法则
$$f'(x) = g'(h(x)) \times h'(x) = sin(x^2) \times 2x$$
$$f'(20)=40sin(400)$$