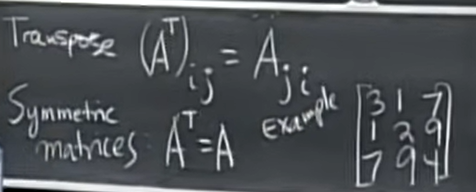标签： 数学

复习一下向量空间（Vector Space）的定义：

向量空间 \(V\) 是一个非空集合，它上的元素称为向量，满足两个运算：加法和数乘，并且得到的结果还在该集合中。

这两个运算必须满足以下 8 条公理（向量空间公理）：

（一）加法的性质u（对任意 \(\mathbf{u}, \mathbf{v}, \mathbf{w} \in V\)）：

1. 交换律： \(\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}\)
2. 结合律：\((\mathbf{u} + \mathbf{v}) + \mathbf{w} = \mathbf{u} + (\mathbf{v} + \mathbf{w})\)
3. 零向量存在性：存在 \(\mathbf{0} \in V\)，使得 \(\mathbf{v} + \mathbf{0} = \mathbf{v}\)
4. 负向量存在性：对每个 \(\mathbf{v} \in V\)，存在 \(-\mathbf{v} \in V\)，使得 \(\mathbf{v} + (-\mathbf{v}) = \mathbf{0}\)

（二）数乘的性质（对任意 \(\mathbf{u}, \mathbf{v} \in V\)）：

5. 结合律：\(a(b \mathbf{v}) = (ab) \mathbf{v}\)
6. 单位元作用：\(1 \cdot \mathbf{v} = \mathbf{v}\)，其中 \(1\) 是乘法单位元
7. 分配律（标量加法）：\(\mathbf{v} = a\mathbf{v} + b\mathbf{v}\)
8. 分配律（向量加法）：\(a(\mathbf{u} + \mathbf{v}) = a\mathbf{u} + a\mathbf{v}\)

矩阵空间的引入

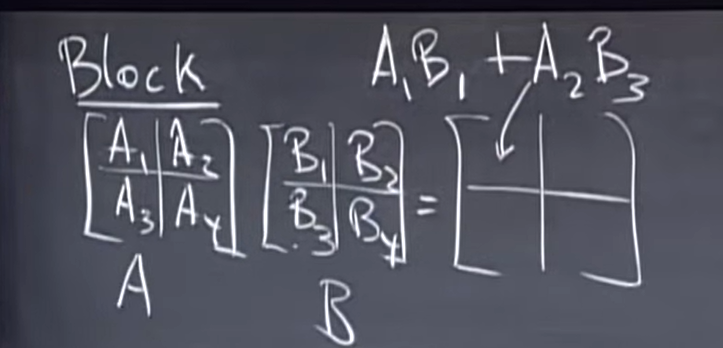
那么，考虑所有\(3 \times 3\)的矩阵，它们其实也构成一个向量空间，因为它们满足上述所有公理。这个向量空间叫做\(3 \times 3\)的矩阵空间，记作\(M_{3 \times 3}(\mathbb R)\)。

\(M_{3 \times 3}(\mathbb R)\)的子空间有：所有\(3 \times 3\)的对称矩阵空间、所有\(3 \times 3\)的上三角矩阵空间等等。

矩阵空间的基

显然，\(M_{3 \times 3}\)的基有\(9\)个。

而\(S\)空间（对称矩阵空间）和\(U\)空间（上三角矩阵空间）作为子空间，它们的维度都是\(6\)。另外，它们的交集维度是\(3\)；它们的和（也就是任意两个的线性组合构成的大空间）的维度是\(9\)，也就是整个空间。

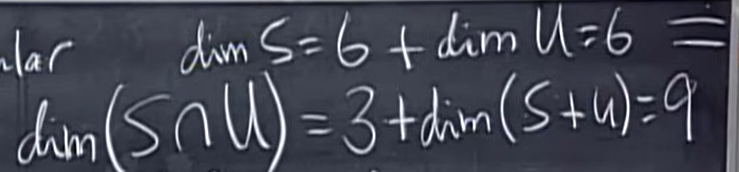
我们很自然地找到了一个公式：\(dim\ S+dim\ U = dim(S\cap U) + dim(S + U)\)

简介

四种子空间分别是：

1. 列空间：\(C(A)\)，在\(R^m\)，维度\(r\)
2. 零空间：\(N(A)\)，在\(R^n\)，维度\(n-r\)
3. 行空间：\(C(A^T)\)，在\(R^n\)，维度\(r\)
4. 左零空间：\(N(A^T)\)，在\(R^m\)，维度\(m-r\)

关于行空间的维度

事实是：\(Dimension\ of\ C(A) = Dimension\ of\ C(A^T) = r\)

一个不太严谨但是很好的说明是：

首先，对\(A\)进行高斯消元，化为主元列只有主元位置是\(1\)的最简形式，此时并不会改变行空间的维度，也不会改变矩阵对应方程组的解集；

我们显然会得到\(r\)个非零行，并且有\(r\)个主元列，因此行空间和列空间的维度都是\(r\)。

关于左零空间

左零空间就是\(N(A^T)\)，也就是说，左零空间是满足\(A^T y = 0\)的\(y\)所在的空间，把整个等式左右两边同时转置得到\(y^T A = 0^T\)，这是一个行向量左乘一个矩阵等于零行向量，因此叫它“左零空间”。

当我们进行行化简后，得到\(EA = R\)形式：

其中\(R\)底部会有一些零行，这些零行正是对应的\(E\)的这些行左乘\(A\)矩阵得到的，也就是说，\(E\)的这些行正是左零空间的基。

总结

现在我们知道了这四种空间，两个在\(R^n\)的空间：行空间和零空间，它们的维度分别是\(r\)和\(n-r\)；两个在\(R^m\)的空间：列空间和左零空间，它们的维度分别是\(r\)和\(m-r\)。

线性无关的定义

称向量\(x_1,x_2,…,x_n\)是线性无关（Linearly independent）的，当它们的线性组合无法产生\(0\)向量（除了所有系数都是零向量的情况）。反之，则称其为线性相关（Linearly dependent）的。

换句话说，线性无关意味着零空间只有零向量；线性相关意味着零空间有非零向量。

空间的基

一个空间的基（Basis）是一些线性无关且能够张成这个空间的向量。

空间的维度

给定一个空间，这个空间的不同的基的向量数量是相同的，而这个数量就是这个空间的维度（Dimension）。

实际上，\(dim(C(A)) = r\)，\(dim(N(A)) = n-r\)。

找到Ax=b的全部解

先解出一个特殊解：\(x_p\)，然后你会发现这个解加上任何一个位于\(Nullspace\)中的向量都是一个解（因为零空间是所有满足\(Ax=0\)的\(x\)集合），也就是说，\(x=x_p+x_n\)。

接着，使用上节课的思路：所有位于零空间的向量就是“把一个自由变量设为1，其他自由变量为0得到的\(Ax=0\)的解”的所有线性组合：

如果我们尝试把它的解集画出来，大概长这样：

它是一个穿过\(x_p\)的平面，但是不一定穿过原点，因此它不是子空间。

满秩矩阵

（如果\(r=n\)，则它是一个列满秩矩阵，解的数量为\(0\)或\(1\)）

（如果\(r=m\)，则它是一个行满秩矩阵，对于任何\(b\)，都存在解。留下了\(n-r\)个自由变量，如果存在自由变量，即\(n-r>0\)，就有无穷多解。）

如果\(r=m=n\)，说明它是可逆矩阵，即有唯一解。

总结

情形	条件	行最简形式 R	解的个数
1	\(r=m=n\)	\(R=I\)	唯一解（1 个）
2	\(r=n<m\)	\(R=\begin{bmatrix}I\\0\end{bmatrix}\)	0 个或 1 个解
3	\(r=m<n\)	\(R=\begin{bmatrix}I & F\end{bmatrix}\)	无穷多解
4	\(r<m, r<n\)	\(R=\begin{bmatrix}I&F\\0&0\end{bmatrix}\)	0 个或无穷多解

矩阵的秩（Rank）是消元后“枢轴”的位置。

进行前向消元后会得到一个阶梯型矩阵，这个例子中我们得到了2个枢轴列和两个自由列。因为我们可以给\(x_2\)和\(x_4\)分配任意值，然后求解出\(x_1\)和\(x_3\)。

零空间就是所有“特殊解”向量所张成的子空间。“特殊解”的意思是把自由变量们赋值为“其中一个是1，其他是0”的形式所得到的方程组解。

简化阶梯型矩阵：

就是每个“枢轴”列只有一个数是\(1\)，其他都是\(0\)的阶梯型矩阵。

其中\(I\)代表单位矩阵，\(F\)代表自由变量们的行和列“分离”出的子矩阵。

列空间

同一向量空间的子空间\(S\)和\(T\)的交集也是一个子空间。

\(A的列空间是所有列向量的线性组合\)。

求\(A\)矩阵的列空间就等同于问“方程\(Ax=b\)对于任意向量x，会得到哪些b？”

我们只能在\(b\)向量在\(A\)矩阵列空间的时候求解出方程\(Ax=b\)。

但是，原矩阵有一个问题：我们可以“丢掉”任意一列，然后得到完全相同的向量空间。因为第三列是前两列的和。如果我们有了前两列，第三列就可以用前两列的某种线性变换表示，第三列就没有任何“新的贡献”。也就是说，第三列是和前两列线性相关的。

零空间（Nullspace）

零空间指的是所有能满足\(Ax=0\)的\(x\)组成的向量空间。

原矩阵的零空间就是所有这种形式的矩阵组成的\(R^3\)的子空间。它是一条在\(R^3\)空间的直线。

总结

这节课主要讲解了得到子空间的两种思路：

1. 找到矩阵的列的线性组合，所有的线性组合构成了一个子空间。（列空间）
2. 找到使\(Ax=0\)方程成立的所有向量\(x\)，所有的\(x\)构成了一个子空间。（零空间）

接着上节课

其中\(P\)是一个行被重新排列的单位矩阵。

\(n \times n\)的矩阵一共有\(n!\)种\(P\)的组合。

对称矩阵：\(A^T=A\)。

\(RR^T\)永远都是对称矩阵。

向量空间

向量空间(Vector Space)是指一堆能相互加，也可以把自身乘以一个标量，最终还会得到一个本空间内的向量的东西。此外，它必须满足8条公理。

比如，\(R^N\)空间是一个向量空间，因为对它进行加和数乘操作是封闭的。

一个向量空间中的向量空间叫做子空间（Subspace）。

\(R^2\)的子空间可以是所有位于一条穿过原点的直线上的向量。

但是这个子空间并不是\(R^1\)，因为它里面的向量都有两个分量。

所有的\(R^2\)的子空间：

1. \(R^2\)本身
2. 任何穿过\((0,0)\)的直线
3. 零向量本身

这个例子中的矩阵的两列的向量，所表示的所有线性组合（即其一的倍数+另一的倍数）被称为列空间(Column space)，顾名思义，就是矩阵的列向量们所张成的一个向量空间，而它们张成的这个列空间一定是\(R^3\)的一个子空间。

也就是说，一个矩阵的列的所有线性组合，张成了一个向量空间，叫做列空间。

\(AB\)的逆是\(B^{-1}A^{-1}\)，这是很显然的（一个很蠢的类比：你穿上袜子再穿上鞋子的逆是你先脱掉鞋子再脱掉袜子）。

另一个公式：

$$(AB)^T=B^T A^T$$

因此

$$(A^{-1})^T=(A^T)^{-1}$$

考虑高斯消元的过程：

（初等矩阵的逆矩阵就是把那个负的变成正的，相当于把减去的那行再加回来）

我们这里已经可以看到L和U的大体“形状”了：L在对角线上全是1，并且是一个正三角形；U是一个倒三角形，对角线上都是我们的“支点”。

三维情况：

如果没有行交换操作，所有的\(E_{??}^{-1}\)会直接“进入”\(L\)中，我们不需要做任何事情，只需要把改的位置都原样放进\(L\)里，就像上面那样。但是反之，所有\(E_{??}\)相乘得到的\(E\)矩阵，就不能这么操作。因为编号较小的行先改变了，编号较大的行才改变，但是编号较大的行需要使用编号较小的行，但此时它已改变。所以上面这个例子中会产生一个我们不喜欢的\(10\)。

可计算出高斯消元的时间复杂度是\(\frac{1}{3} n^3\)。

行交换的初等矩阵记作\(P\)，而3维中\(P\)的所有组合如下：

一个\(3\times 3\)的矩阵只有6个不同的\(P’s\)。

这些矩阵很特殊：它们互相无论怎么乘，都会得到一个在这个列表中的一个矩阵，同样，它们的逆矩阵也在列表中。这些矩阵组成了一个群（Grup）。并且，\(P^{-1}=P^T\)。

矩阵乘法

若\(AB=C\)，则

角度1：

$$C_{i,j}=(row\ i\ of\ A) \cdot (column\ j\ of\ B)$$

角度2,3：

角度4：

首先考虑，用A的一列乘B的一行会得到什么？

这是一个\(m \times 1\)的矩阵乘一个\(1\times p\)的矩阵，所以会得到一个\(m \times p\)的矩阵，并且得到的这个矩阵非常特殊，因为它的行列空间都分别在一条直线上。

而第4种角度就是：

$$C = \sum_{i=1}^n(column\ i\ of\ A) \cdot (row\ i\ of\ B)$$

角度5：

“分块”

$$C_{ij} = \sum_{k=1}^n A_{ik} B_{kj}$$

这种思想被广泛应用于GPU并行计算等场合。

逆矩阵

一个矩阵的逆矩阵要保证

$$A^{-1}A = I = AA^{-1}$$

但并不是每个矩阵都有逆矩阵，没有逆矩阵的矩阵称为“奇异矩阵”。

首先，如果原矩阵不是方阵，就不存在逆矩阵。

然后，如果存在某个非零向量x，使得\(Ax=0\)，A就不存在逆矩阵。因为如果它存在，我们会解出\(x=0\)，但实际上x非零。

高斯消元法：

对AI增广矩阵进行若干次行初等变换（就像之前文章说的那样，行初等变换操作就相当于左乘一个初等矩阵，对增广矩阵进行操作是为了方便把等号左右两边同时操作），我们先会得到一个“倒三角形矩阵”（这是因为我们只消除了左下这一个三角形的数）；然后，通过回代的方式，只让对角线有数字；最后，把对角线上的数都归一。这样进行若干次行初等变换后，\(A\)变成了\(I\)，同理\(I\)就变成了\(A^{-1}\)