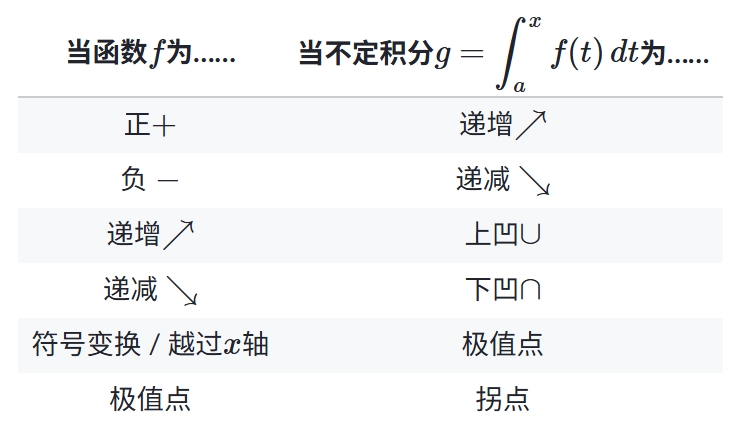
此文我们将先探讨线性组合的基本定义(公式为主),然后再思考它的几何层面含义。
基本定义
线性方程组是形式如下的方程组: \(
a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = b_1 \\
a_{21}x_1 + a_{22}x_2 + a_{23}x_3 = b_2 \\
a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = b_3
\)
“线性”表示它的含字母项的次数都是1。
它可以写成矩阵形式: \(\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}\)
把系数矩阵叫做 A,未知数向量叫做 x,结果常数向量叫做b,原线性方程组可改写为:
$$A \cdot x = b$$
非常的简洁。
(如果你还不清楚矩阵乘向量的代数计算方法,请到文章最后一部分)
横纵考虑矩阵
横向
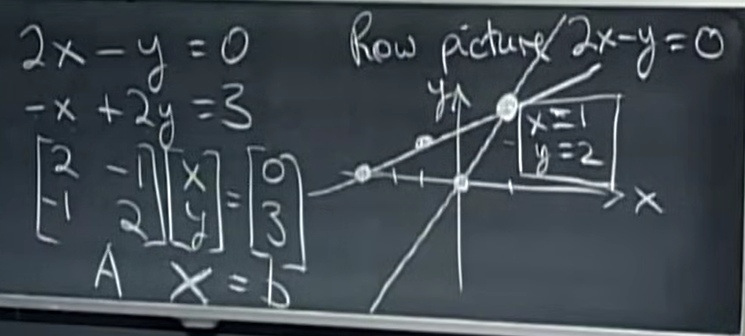
如上图所示,当我们“横向”考虑这个矩阵(也就是二元线性方程组)时,方程组的解就是每个方程所对应的直线(这也是它叫做“线性方程”的原因——方程的图像都是直线)的交点:\((1, 2)\)。
纵向
那么,如果我们“纵向”考虑那个矩阵,会发现什么呢?
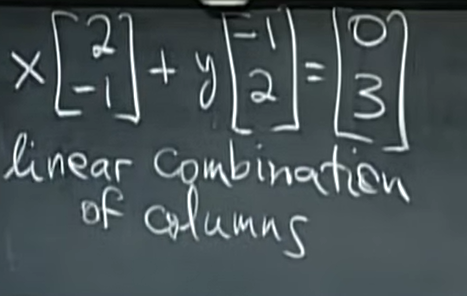
如上图,我们会得到一个整齐的式子:A的第一列向量乘第一个未知数 + A的第二列向量乘第二个未知数 = 结果常数向量b。
矩阵乘以向量就被称为列的线性组合。
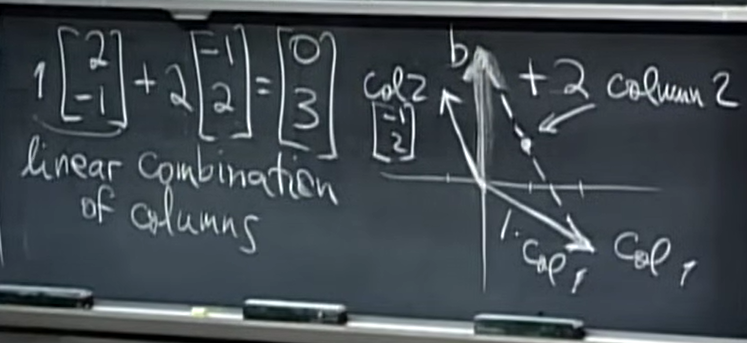
在几何坐标系中画出两个向量\(\begin{bmatrix} 2 \\ -1 \end{bmatrix}\)和\(\begin{bmatrix} -1 \\ 2 \end{bmatrix}\),由于我们已经解出了\(x=1, y=2\),因此我们可以把\(\begin{bmatrix} 1 \\ 2 \end{bmatrix}\)代入到原先\(\begin{bmatrix} x \\ y \end{bmatrix}\)的地方,看看最后是否得到了b,就像图中画的那样,最后得到的向量加法结果恰好就是\(\begin{bmatrix} 0 \\ 3 \end{bmatrix}\)这个向量,也就是b。
如果x和y是未知数,在大多数情况下,经过线性组合后,x和y经过线性组合后的结果会充满整个二维平面,也就是说任何二维向量都可以被x, y经过这个线性组合所描述。
说到这里,就不得不提基向量了。在二维物理问题中,我们会把一个向量写成\(a \cdot \hat{i} + b \cdot \hat{j}\)的形式,其中
$$ \hat{\imath} = \begin{bmatrix} 1 \\ 0 \end{bmatrix},\quad \hat{\jmath} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} $$
那么如果我们把\(\hat{i} \)和\(\hat{j} \)改变为其他向量会发生什么?也就是,如果我们把坐标系的基改变,会发生什么?
聪明的你一定发现了:线性组合的本质实际上就是改变基!矩阵乘向量,就意味着对向量做这个矩阵所描述的线性变换,也就是,在以该矩阵所描述的基向量的“坐标系”下,这个向量所对应的那个向量在原坐标系中的向量值。
矩阵的第 \(i\)列,就表示第\(i\)个轴上的基向量改变成了什么向量。
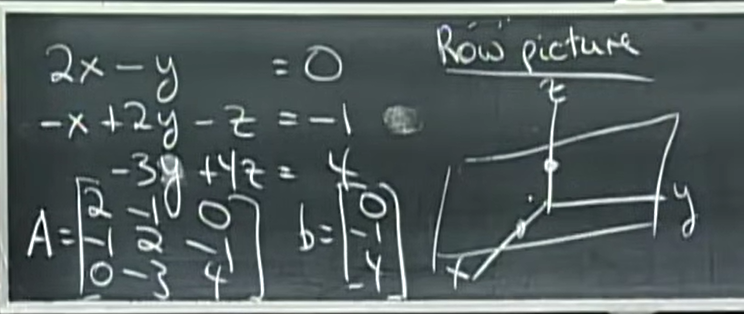
考虑三维情况:3个未知数和3个方程构成的线性方程组。我们也可以把它写成图中的矩阵形式:
\(\begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0\\ -1 \\4 \end{bmatrix}\)
横向
还是先横向考虑:考虑其中一个线性方程,比如第二个,我们会得到一个平面(所有满足该方程组的解都在一个处于三维空间的二维平面上)。

若同时考虑两个方程,所有满足条件的点就是两个平面相交所产生的直线。

同时考虑三个方程,满足条件的点只有一个:三个平面的交点。
纵向

如果纵向考虑该矩阵,我们会得到这样的线性组合形式:
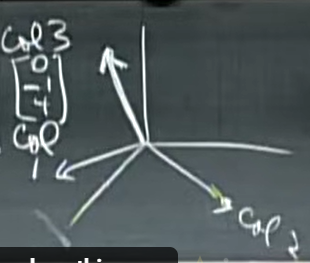
这三个就是新的基向量。
它的解可以被直接看出来,也就是 \(x=0, y=0, z=1\)的时候。
思考:一个\(n \times n\)方阵的线性组合总是能生成任何一个n维向量吗?
答案为:不一定。在大多数情况下,确实是这样的,但是在某些 情况下,由于矩阵列之间的线性依赖(某个基向量可以被其他基向量的组合表示),会导致线性变换所能生成的空间降维,因此不一定。
补充-矩阵乘向量
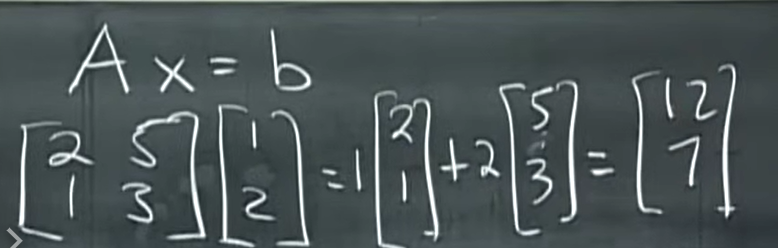
矩阵乘向量就是线性组合(也叫线性变换),而它的计算方式的符号表示法就是用向量的第1个数乘矩阵的第1列 加上 向量的第2个数乘矩阵的第2列,这样计算下去。
当然,也可以用点积的思想, 矩阵的第1行与向量的点积得到结果的第1个数,矩阵的第2行与向量的点积得到结果的第2个数。